
Las leyes de Kirchhoff fueron formuladas por Gustav Kirchhoff en 1845, mientras aún era estudiante. Tanto la primera como la segunda ley de Kirchhoff son muy utilizadas en ingeniería eléctrica para obtener los valores de la corriente y el potencial en cada punto de un circuito eléctrico. Surgen de la aplicación de la ley de conservación de la energía.

Leyes de Kirchhoff
Para comenzar a analizar las leyes de Kirchhoff, diremos primeramente que en un circuito eléctrico, es común que se generen nodos de corriente. Un nodo o nudo es el punto del circuito donde se unen mas de un terminal de un componente eléctrico.
Primera Ley de Kirchhoff
Se puede generalizar la Primera Ley de Kirchhoff diciendo que la suma de las corrientes entrantes a un nodo son iguales a la suma de las corrientes salientes.
Si se le asigna signos (+ y -) a las corriente del circuito, positivo las corrientes que entran y negativo las corrientes que salen, entonces, la sumatoria de las corrientes que convergen en un nodo es igual a cero.
Ley de nodos
En un circuito cerrado:
“La corriente entrante a un nodo es igual a la suma de las corrientes salientes”.
Σ I = 0
La razón por la cual se cumple esta ley se entiende perfectamente en forma intuitiva si uno considera que la corriente eléctrica es debida a la circulación de electrones de un punto a otro del circuito.
Piense en una modificación de nuestro circuito en donde los resistores tienen un valor mucho más grande que el indicado, de modo que circule una corriente eléctrica muy pequeña, constituida por tan solo 10 electrones que salen del terminal positivo de la batería.
Los electrones están guiados por el conductor de cobre que los lleva hacia el nodo 1. Llegados a ese punto los electrones se dan cuenta que la resistencia eléctrica hacia ambos resistores es la misma y entonces se dividen circulando 5 por un resistor y otros 5 por el otro.
Esto es totalmente lógico porque el nodo no puede generar electrones ni retirarlos del circuito solo puede distribuirlos y lo hace en función de la resistencia de cada derivación.
En nuestro caso las resistencias son iguales y entonces envía la misma cantidad de electrones para cada lado. Si las resistencias fueran diferentes, podrían circular tal vez 1 electrón hacia una y nueve hacia la otra de acuerdo a la aplicación de la ley de Ohm.
Ley de conservación de la energía
Mas científicamente podríamos decir, que siempre se debe cumplir una ley de la física, a la que suele denominarse Ley de la Conservación de la Energía. Esta dice que la energía no se crea ni se consume, sino que siempre se transforma.
La energía eléctrica que entrega la batería se subdivide en el nodo de modo que se transforma en iguales energías térmicas entregadas al ambiente por cada uno de los resistores. Si los resistores son iguales y están conectados a la misma tensión, deben generar la misma cantidad de calor y por lo tanto deben estar recorridos por la misma corriente; que sumadas deben ser iguales a la corriente entregada por la batería, para que se cumpla la ley de conservación de la energía.
En una palabra, que la energía eléctrica entregada por la batería es igual a la suma de las energías térmicas disipadas por los resistores.
Aplicación de la Primera Ley de Kirchhoff
En la primera figura se puede observar el mas básico de los circuitos de corriente continua (CC) que contiene dos nodos.
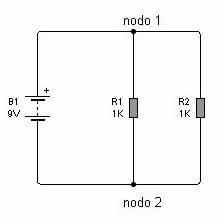
Observe que se trata de dos resistores de 1K (R1 y R2) conectados sobre una misma batería B1.
La batería B1 conserva su tensión fija a pesar de la carga impuesta por los dos resistores; esto significa cada resistor tiene aplicada una tensión de 9V sobre él.
La ley de Ohm indica que cuando a un resistor de 1K se le aplica una tensión de 9V por el circula una corriente de 9 mA.
I = E/R = 9/1.000 = 0,009 A = 9 mA
Por lo tanto podemos asegurar que cada resistor va a tomar una corriente de 9 mA de la batería o que entre ambos van a tomar 18 mA de la batería.
También podríamos decir que desde la batería sale un conductor por el que circulan 18 mA que al llegar al nodo 1 se bifurca en una corriente de 9 mA que circula por cada resistor, de modo que en el nodo 2 se vuelven a unir para retornar a la batería con un valor de 18 mA.
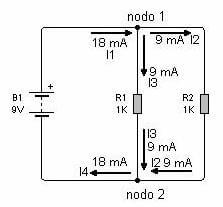
Es decir que en el nodo 1 podemos decir que I1 = I2 + I3 y reemplazando valores: que 18 mA = 9 mA + 9 mA y que en el nodo 2, I4 = I2 + I3.
Las corriente I1 e I4 son iguales porque lo que egresa de la batería debe ser igual a lo que ingresa.
Segunda Ley de Kirchhoff
La aplicación de la segunda Ley de Kirchhoff (Gustav Kirchhoff 1824-1887) se utiliza cuando un circuito posee mas de una batería y varios resistores de carga. En este caso, ya no resulta tan claro como se establecen la corriente por el mismo. En ese caso es de aplicación de esta ley la que nos permite resolver el circuito con una gran claridad.
Ley de mallas
En un circuito cerrado:
“La suma de las tensiones de batería que se encuentran al recorrerlo siempre serán iguales a la sumatoria de las caídas de tensión existente sobre los resistores”.
Σ I * R = 0
Aplicación de la Segunda Ley de Kirchhoff
En la siguiente figura se puede observar un circuito con dos baterías que nos permitirá resolver un ejemplo de aplicación.
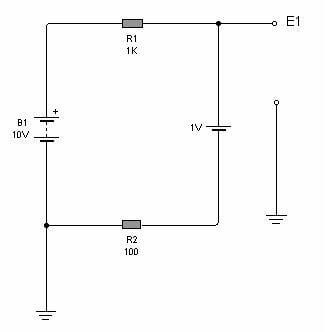
Observe que el circuito posee dos baterías y dos resistores. Nosotros deseamos saber cual es la tensión de cada punto (o el potencial), con referencia al terminal negativo de B1 al que le colocamos un símbolo que representa a una conexión a nuestro planeta y al que llamamos tierra o masa.
Esto es porque podemos considerar al Planeta Tierra como un inmenso conductor de la electricidad.
Las tensiones de fuente, simplemente son las indicadas en el circuito, pero si pretendemos aplicar las caídas de potencial en los resistores, debemos determinar primero cual es la corriente que circula por aquel.
Para determinar la corriente, primero debemos determinar cuál es la tensión de todas nuestras fuentes sumadas.
Observe que las dos fuentes están conectadas de modos que sus terminales positivos están galvánicamente conectados entre si por el resistor R1. Esto significa que la tensión total no es la suma de ambas fuentes sino la resta.
Con referencia a tierra, la batería B1 eleva el potencial a 10V pero la batería B2 lo reduce en 1V. Entonces, la fuente que hace circular corriente es en total de 10 – 1 = 9V.
Los electrones que circulan por ejemplo saliendo de B1 y pasando por R1, luego pierden potencial en B2 y atraviesan R2. Para calcular la corriente circulante podemos agrupar entonces a los dos resistores y a las dos fuentes tal como lo indica la siguiente figura.
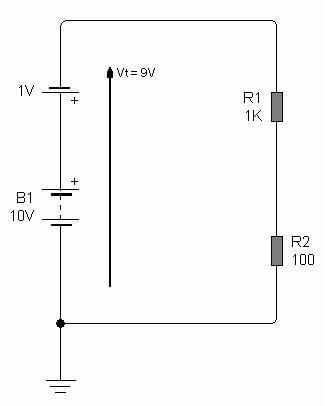
¿Los dos circuitos anteriores son iguales?
No, este reagrupamiento solo se genera para calcular la corriente del circuito original.
De acuerdo nuevamente a la ley de Ohm:
I = E / R1 + R2
Porque los electrones que salen de R1 deben pasar forzosamente por R2 y entonces es como si existiera un resistor total igual a la suma de los resistores R1 + R2 = 1100.
Se dice que los resistores están conectados en serie cuando están conectados de este modo. De forma tal que ambos son atravesados por la misma corriente igual a:
I = (10 – 1) / 1000 + 100 = 0,00817 o 8,17 mA.
Cálculo del circuito resultante
Ahora que sabemos cual es la corriente que atraviesa el circuito podemos calcular la tensión sobre cada resistor.
De la expresión de la ley de Ohm (I = E/R), se puede despejar que E = R . I y de este modo reemplazando valores se puede obtener que la caída sobre R2 es igual a ER2 = R2 . I = 100 . 8,17 mA = 817 mV y del mismo modo ER1 = R1 . I = 1000 . 8,17 mA = 8,17 V.
Estos valores recién calculados de caídas de tensión pueden ubicarse sobre el circuito original con el fin de calcular la tensión deseada.
Circuito resulto con la Segunda Ley de Kirchhoff
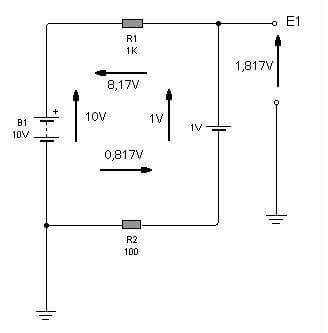
Observando las cuatro flechas de las tensiones de fuente y de las caídas de tensión se puede verificar el cumplimiento de la segunda Ley de Kirchhoff. Ya que comenzando desde la masa de referencia y girando en el sentido de las agujas del reloj podemos decir que:
10V – 8,17V – 1V – 0,817 = 0V
O, realizando una transposición de términos y dejando las fuentes a la derecha y las caídas de tensión a la izquierda podemos decir que la suma de las tensiones de fuente 10V – 1V es igual a la suma de las caídas de tensión o diferencias de potencial 8,17V + 0,817 = 8,987 aproximadamente 9V.
Y además podemos calcular fácilmente que la tensión sobre la salida del circuito es de 0,817V + 1V = 1,817V con la polaridad indicada en el circuito es decir positiva.
Conclusión
Las dos leyes de Kirchhoff son igualdades que se basan en el principio de la conservación de la energía y la carga en los circuitos eléctricos, y como dijimos al comienzo, son utilizadas para hallar corrientes y tensiones en cualquier punto de un circuito eléctrico. Ambas leyes de circuitos pueden derivarse directamente de las ecuaciones de Maxwell, pero Kirchhoff lo hizo primero. Gracias a Georg Ohm su trabajo fue generalizado y actualmente son ampliamente utilizadas tanto en electricidad como en electrónica.

