
Medir significa comparar una magnitud, de valor desconocido, con una magnitud de referencia de igual especie, previamente elegida, que se denomina unidad de medida.
El inconveniente es que los resultados de las mediciones no son exactos. Por mas cuidado que se tenga en todo el proceso de la medición, es imposible que el resultado de la misma sea exacto. Surge entonces el error de medición. Se debe considerar que aún los patrones tienen error.
Veamos a continuación en qué consiste el error de medición, cómo se mide o estima y de qué manera pueden corregirse según de qué tipo de error se trate.
El error absoluto
Se llama error absoluto (Ea) a la diferencia entre el valor medido (Vm) y el valor verdadero (Vv) de la respectiva magnitud.
Es decir:
| Error absoluto |
|---|
| Ea = Vm - Vv |
El concepto de error absoluto no nos da una idea clara de la exactitud de la medición efectuada. Por ejemplo, es muy distinto cometer un error de 10 V al medir 13200 V, que al medir 220 V.
Sin embargo, el valor verdadero es casi imposible de conocer.
El error absoluto convencional
En la práctica puede tomarse como valor verdadero al hallado a través de un muestreo estadístico de un gran número de mediciones. En este caso, el valor se denomina valor verdadero convencional (Vvc), y el error correspondiente es el error absoluto convencional (Eac):
| Error absoluto convencional |
|---|
| Eac = Vm - Vvc |
De las fórmulas anteriores se desprende que el error de medición absoluto será positivo cuando se mida en exceso y negativo cuando se lo haga en defecto.
De aquí en más, por simplicidad, tomaremos como valor verdadero al valor verdadero convencional (Vvc).
Error de medición relativo
Como dijimos anteriormente, el error absoluto no nos da una idea clara de la exactitud de la medición. Por lo tanto, es conveniente asociar el error absoluto al valor verdadero, o aquel tomado como tal, para poder comparar los resultados de las mediciones efectuadas.
Lo que se obtiene es el error relativo (Er) en tanto por uno:
| Error relativo |
|---|
| Er = Ea / Vv = (Vm - Vv) / Vv |
En valores porcentuales:
| Error relativo porcentual |
|---|
| Er% = Ea . 100 / Vv = (Vm - Vv) . 100 / Vv |
Cabe señalar que el error de medición típico de una medición destinada a un tablero eléctrico ronda el 1,5%, la de un laboratorio de ensayos fabriles es del 0,5% y la de un laboratorio de calibración es menor del 0,1%.
Tipos de errores en una medición

Antes de realizar una medición con un grupo de instrumentos dados, es importante determinar qué tipos de errores pueden presentarse en la medición, para saber si se está dentro de nuestros requerimientos de exactitud.
El estudio a fondo de la teoría de errores excede los alcances de este artículo y por lo tanto no se efectuará. Si bién no es fácil realizar una clasificación estricta, en los párrafos siguientes se presentará la clasificación clásica de los errores.
Según la misma, los tipos de errores en una medición se pueden clasificar en ✅ errores groseros, ✅ errores sistemáticos y ✅ errores aleatorios (al azar).
Errores groseros
Los errores groseros consisten en equivocaciones en las lecturas y registros de los datos. En general se originan en la fatiga del observador, en el error al transcribir los valores medidos a las planillas de los protocolos de ensayos, a la desconexión fortuita de alguna parte del circuito de medición, etcétera.
Estos errores se caracterizan por su gran magnitud, por lo que suelen ser fácilmente detectables al comparar varias mediciones de la misma magnitud. La forma más recomendable de disminuir los errores groseros en una medición consiste en realizar al menos 3 (tres) mediciones repetidas.
Errores sistemáticos
Se llaman errores sistemáticos porque se repiten sistemáticamente en el mismo valor y sentido en todas las mediciones que se efectúan en iguales condiciones.
Las causas de estos errores están perfectamente determinadas y pueden ser corregidas mediante ecuaciones matemáticas que eliminen el error. En algunos casos pueden emplearse distintos artificios que hacen que la perturbación se autoelimine.
En virtud de las causas que originan los errores sistemáticos, es conveniente realizar una subdivisión:
1. Errores de ajuste, o errores que introducen los instrumentos
Estos errores son debidos a las imperfeciones en el diseño y construcción de los instrumentos. Mediante la calibración durante la construcción, se logra que para determinadas lecturas se haga coincidir las indicaciones del instrumento con valores obtenidos con un instrumento patrón local.
Sin embargo, por limitaciones técnicas y económicas, no se efectúa ese proceso en todas las divisiones de la escala. Esto origina ciertos desajustes en algunos valores de la escala, que se mantienen constantes a lo largo del tiempo.
Estos errores de medición repetitivos pueden ser medidos en módulo y signo a través del contraste, que es un ensayo consistente en comparar simultáneamente la indicación del instrumento con la indicación de un instrumento patrón de la mas alta calidad metrológica (cuya indicación representa el valor verdadero convencional).
2. Errores de método, o errores debidos a la conexión de los instrumentos
Los errores de método se originan en el principio de funcionamiento de los instrumentos de medición. Hay que considerar que el hecho de conectar un instrumento en un circuito, siempre origina algún tipo de perturbación en el mismo. Por ejemplo, en los instrumentos analógicos aparecen los errores de consumo, fase, etcétera.
Para corregir estos errores deben determinarse las características eléctricas de los instrumentos (resistencia, inductancia y capacidad). En algunos casos es posible el uso de sistemas de compensación, de forma tal de autoeliminar el efecto perturbador.
Por ejemplo, en el caso del wattímetro compensado, que posee un arrollamiento auxiliar que contrarresta la medición del consumo propio.
3. Errores por efecto de las magnitudes de influencia, o errores por causas externas
El medio externo en que se instala un instrumento influye en el resultado de la medición. Una causa perturbadora muy común es la temperatura, y en mucha menor medida, la humedad y la presión atmosférica.
La forma de eliminar este error de medición es mediante el uso de las ecuaciones físicas correspondientes. En los instrumentos de precisión, suelen venir indicadas en la chapa que contiene la escala del mismo.
En algunos casos, los instrumentos disponen de artificios constructivos que compensan la acción del medio externo. Por ejemplo, la instalación de resortes arrollados en sentidos contrarios, de manera que la dilatación térmica de uno de ellos se contrarresta por la acción opuesta del otro.
Por otra parte, la mejora tecnológica de las aleaciones utilizadas ha reducido mucho los efectos debidos a la acción de la temperatura ambiente.
4. Errores por la modalidad del observador, o ecuación personal
En este último caso, cada observador tiene una forma característica de apreciar los fenómenos, y en particular, de efectuar lecturas en las mediciones. Lo curioso que nos muestra la experiencia, es que cada observador repite su modalidad en forma sistemática. De allí que se denomine a esta característica ecuación personal.
Por ejemplo, al medir tiempos un determinado observador registra los mismos con adelanto o retraso con respecto a otro observador.
Errores aleatorios
Es un hecho conocido que al repetir una medición utilizando el mismo proceso de medición (el mismo instrumento, operador, excitación, método, etc.) no se logra el mismo resultado.
En este caso, los errores sistemáticos se mantienen constantes, y las diferencias obtenidas se deben a efectos fortuitos, denominados errores aleatorios (mal llamados accidentales).
Por ello, una característica general de los errores aleatorios es que no se repiten siempre en el mismo valor y sentido.
En virtud de las causas que originan este tipo de error, es conveniente realizar una subdivisión de los errores aleatorios:
1. Rozamientos internos
En los instrumentos analógicos se produce una falta de repetitibilidad en la respuesta, debido fundamentalmente a rozamientos internos en el sistema móvil. Asimismo, los falsos contactos también dan lugar a la aparición de este tipo de error.
2. Acción externa combinada
Muchas veces la compleja superposición de los efectos de las distintas magnitudes de influencia no permiten el conocimiento exacto de la ley matemática de variación del conjunto, por ser de difícil separación. De esta manera, no puede predecirse el error ni realizarse las correcciones debidas, convirtiéndose en un error aleatorio.
3. Errores de apreciación de la indicación
En muchas mediciones, el resultado se obtiene por la observación de un índice (o aguja) en una escala, originándose así error de medición en la apreciación.
Estos a su vez tienen dos causas diferentes:
3.1 Error de paralaje
Se origina en la falta de perpendicularidad entre el rayo visual del observador y la escala respectiva. Esta incertidumbre se puede reducir con la colocación de un espejo en la parte posterior del índice. Así la perpendicularidad del rayo visual se logrará cuando el observador no vea la imagen del mismo en el espejo.
3.2 Error del límite separador del ojo
El ojo humano normal puede discriminar entre dos posiciones separadas a más de 0,1 mm, cuando se observa desde una distancia de 300 mm. Por lo tanto, si dos puntos están separados a menos de esa distancia no podrá distinguirlos.
La magnitud de este error es típicamente subjetiva, pues hay personas que tienen una visión mejor o peor que la normal.
Para disminuir este tipo de error se puede recurrir al uso de lentes de aumento en las lecturas.
4 Errores de truncamiento
En los instrumentos provistos con una indicación digital, la representación de la magnitud medida está limitada a un número reducido de dígitos.
Por lo tanto, en tales instrumentos no pueden apreciarse unidades menores que la del último dígito del visor (o display), lo que da lugar a un error por el truncamiento de los valores no representados.
La magnitud máxima de este tipo de error dependerá del tipo de redondeo que tenga el instrumento digital, siendo el 50% del valor del último dígito representado para el caso de redondeo simétrico y el 100% para el caso del redondeo asimétrico.
Ejemplo de corrección de error
La siguiente animación muestra cómo leer calibradores cuando hay un "error cero".
Suponemos que la pinza debe leer 0,00 mm cuando las mordazas están cerradas completamente, pero la pinza de la animación muestra una lectura de +0,10 mm en esta situación.
A este error de medición se denomina "error cero" del calibrador, que en general puede ser cero, positivo, o también negativo. Dado que en el ejemplo, todas las mediciones con este calibrador sobrestiman las longitudes en +0,10 mm (ver error sistemático), el error cero se debe restar de todas las mediciones de longitud.
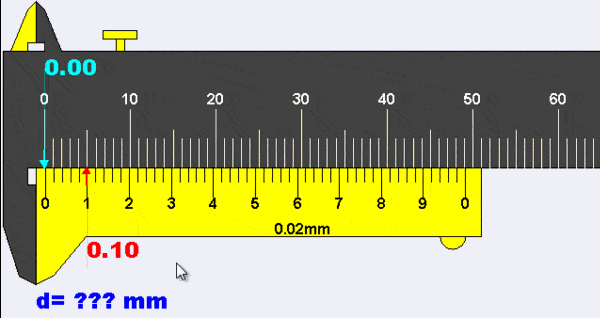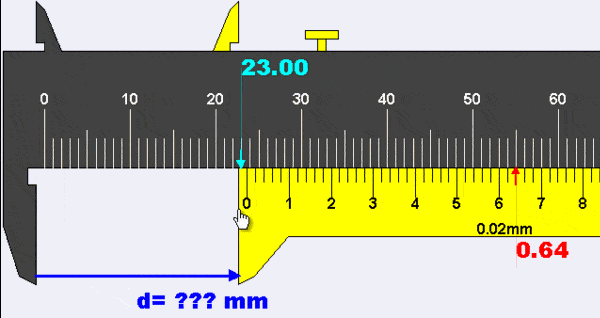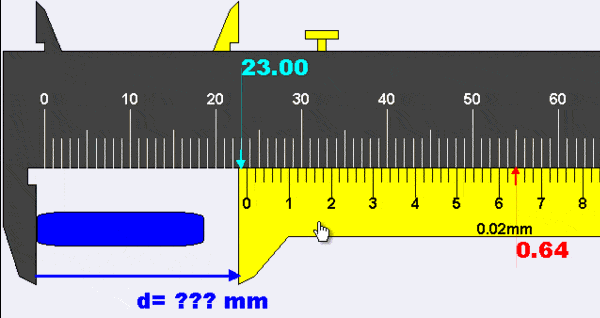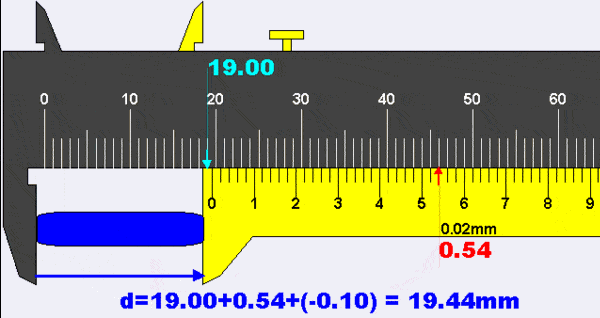
La fórmula para una lectura adecuada de un calibre es:
| Lectura real = Escala principal + Escala de nonio - error cero |
|---|
| lectura real = 19,00 + 0,54 - (-0,10) = 19,44 mm |
En la animación, la lectura de la escala principal es 19,00 mm y la lectura de la escala nonio* es 0,54 mm. El error del instrumento es el ancho del subintervalo más pequeño, que en este caso es de 0,02 mm. La lectura completa se puede expresar como 19,44 mm ± 0,02 mm.
* El nonio o escala de Vernier es una segunda escala auxiliar que tienen algunos instrumentos de medición, que permite apreciar una medición con mayor exactitud o con menor error de medición, al complementar las divisiones de la regla o escala principal del instrumento de medida. (Wikipedia)
Clase en Video sobre errores de medición
En este caso, tenemos un video de la clase de física para el primer grado del bachillerato en España y trata sobre el concepto de medición y la teoría sobre errores en la medida.

